用前必读
1，使用excel存储并调整数据，然后拷贝、粘贴到输入框
2，先用输入框下方的“输入检查”按钮检查输入，通过后再作图
3，表头请勿使用#，<，>，%，(，)等特殊符号。默认仅支持英文字符
4，使用inkscape或者AI修改文字、字体，图例，处理截断
5，生信项目合作，提交bug、发文引用换积分，请加管理员微信（页面右下）

人工客服   基因名转换   FC,P转换   常用配色 需求及bug提交   pdf转图片
必需输入  PCA绘制视频教程   文字教程
缺失值用NA代替，但是不能为空，程序自动impute
若行名有重复，使用合并工具预处理后再绘图
数据较少（直接拷贝数据并粘贴到输入框）

数据较多（上传tab分割的txt文件）

可选输入
图片大小
图片宽度：；图片高度：

文字及字体大小
点大小：；点标注文字字体大小：
轴说明文字字体大小：；轴刻度数字字体大小：
图例标题：
图例标题字体大小：；图例文字字体大小：

颜色（10种自定义，20种默认。即最多绘制30组）
颜色1： ；颜色2：
颜色3： ；颜色4：
颜色5： ；颜色6：
颜色7： ；颜色8：
颜色9： ；颜色10：

是否加样名名标注


是否添加椭圆等形状（注：椭圆要求至少4个点）





字体


主成分分析（PCA）

简介
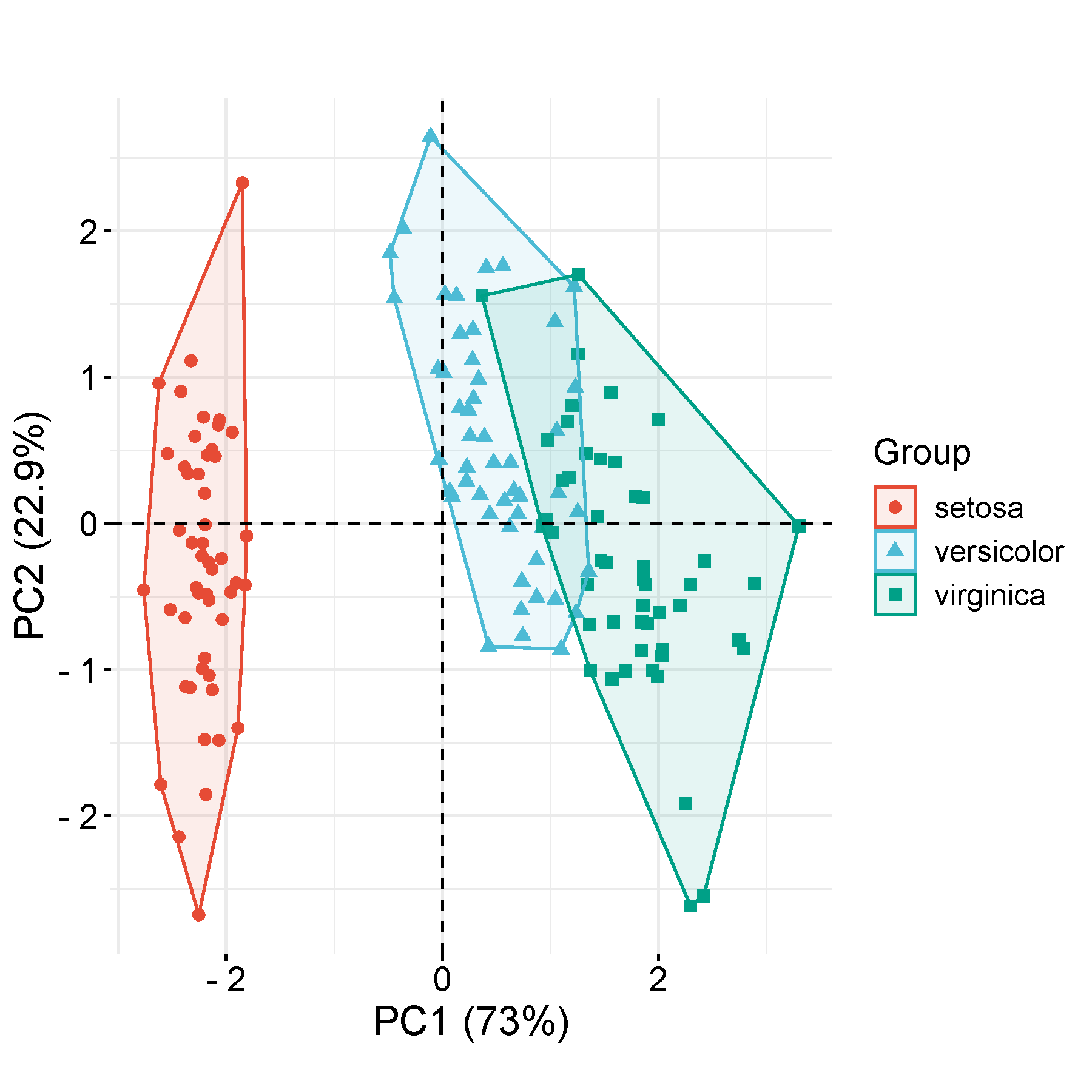
主成分分析（Principal component analysis，PCA）利用正交变换对一系列可能相关的变量的观测值进行线性变换，从而投影为一系列线性不相关变量的值，这些不相关变量称为主成分（Principal Components）。PCA是最简单的以特征量分析多元统计分布的方法。通常情况下，这种运算可以被看作是揭露数据的内部结构，从而更好的解释数据的变量的方法。
数据说明
行为特征（例如基因，蛋白，代谢物等），列为样品。第一行为样品名，第二行为组名，第3+行为特征。图中坐标轴Dim1和Dim2为第一、第二主成分（即潜在变量对差异的解释率）；点代表样品（individuals），不同颜色表示不同分组。调用：prcomp计算PCA，FactoMineR包绘图。
该包默认对数据进行center和scale转化。
论文例子
[Nature communications] Sympathetic axonal sprouting induces changes in macrophage populations and protects against pancreatic cancer. Fig4h
输入 示例数据
输出

如何引用？

建议直接写网址。助力发表5800+篇（google学术），5000+篇（知网）论文
正式引用：Tang D, Chen M, Huang X, Zhang G, Zeng L, Zhang G, Wu S, Wang Y.SRplot: A free online platform for data visualization and graphing. PLoS One. 2023 Nov 9;18(11):e0294236. doi: 10.1371/journal.pone.0294236. PMID: 37943830.
方法章节：Heatmap was plotted by https://www.bioinformatics.com.cn (last accessed on 10 Dec 2024), an online platform for data analysis and visualization.
致谢章节：We thank Mingjie Chen (Shanghai NewCore Biotechnology Co., Ltd.) for providing data analysis and visualization support.